The Discounted Cash Flow Model (DCF Model) is a valuation method used to estimate the value of an investment based on its expected future cash flows. By discounting the predicted cash flows to the present value, it accounts for the time value of money, acknowledging that funds received in the future are worth less than the same amount received today.
This page covers the following topics related to the DCF Model:
General Formula
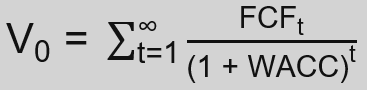
- Value of the firm (V0): Total present value of the company in year 0
- Free Cash Flows (FCFt): Available cash after covering operating expenses and capital investments (i.e. Free Cash Flow to the Firm)
- Weighted Average Cost of Capital (WACC): Weighted average of the cost of a company’s equity and debt capital.
The DCFM estimates the present value of future cash flows by applying the Weighted Average Cost of Capital (WACC) as a discount rate. The calculation of the model involves summing the present values of future FCF, each discounted back to the present, where FCFt is the free cash flow in period t. The model integrates the time value of money concept, emphasizing that future cash flows are worth less in today’s terms.
DCF Model with Terminal Value
In practice, it is typically not feasible to forecast FCFs for an infinite number of periods. Thus, the discounted value of the FCFs beyond the forecast period are typically expressed as terminal value (TV).

- Terminal Value (TV): Present value of all future free cash flows to pay beyond a forecast period T.
The practical importance of the terminal value (TV) is crucial, as it often constitutes a substantial portion of the final valuation. This is especially true for companies with long-term growth prospects, where a significant portion of value generation may occur beyond the forecasting period.
There are two main approaches to calculating the terminal value (TV): (1) the Gordon Growth Model (GGM) and (2) the Exit Multiple Method. The choice between these methods depends on several factors, including the stability of the long-term growth rate and whether the intent is to hold the company indefinitely or sell it at the end of the forecasting period.

- Free Cash Flows (FCFT): FCF in the final forecasting period T
- Growth Rate (g): represents the constant growth rate of free cash flows expected after year T
The use of the Gordon Growth Model requires careful estimation of assumptions, as its outcome is highly sensitive to the long-term growth rate. It is advisable to adopt a conservative estimate for g, which should not exceed the long-term GDP growth rate.
Alternatively, the TV can be calculated using the Exit Multiple Method. This approach involves selecting an appropriate multiple, estimating its value in period T based on comparable companies, and then applying it to the corresponding forecasted financial metric (e.g., EBITDA, EBIT, revenue) of the company in period T.
TV = EBITDA MultipleT * Company EBITDAT
TV = EBIT MultipleT * Company EBITT
TV = Revenue MultipleT * Company RevenueT
- MultipleT: Median multiple of comparable companies forecasted in period T
- Financial MetricT: Forecasted financial metric for period T that corresponds to the select mulitple
Calculating Equity Value
The DCF model determines the total value of the firm (V), provided one utilizes free cash flow to the firm (FCFF) and the weighted average cost of capital (WACC). To derive the value of equity (A), subtract the net debt (ND) from the firm’s total value.
A0 = V0 – ND0
- Value of Equity (A0): Total present value of equity in year 0
- Value of the firm (V0): Total present value of the firm in year 0.
- Net debt (ND0): Financial debt minus cash and cash equivalents in year 0.
In practice, the DCF Model is crucial in finance, particularly in the areas of investment analysis, capital budgeting, and valuation of companies. The DCF Model is widely used due to its detailed and fundamental approach to valuation, but its accuracy heavily relies on the precision of the assumptions for future cash flows and the discount rate.
Related Topics
Disclaimer: The information provided on this website is for educational purposes only and is not intended for use as legal, financial, or tax advice. While every effort is made to ensure the accuracy and reliability of the content, Maths for Finance makes no representations or warranties of any kind, express or implied, about the completeness, accuracy, reliability, suitability, or availability with respect to the website or the information, products, services, or related graphics contained on the website for any purpose. Any reliance you place on such information is therefore strictly at your own risk. In no event will Maths for Finance be liable for any loss or damage including without limitation, indirect or consequential loss or damage, or any loss or damage whatsoever arising from loss of data or profits arising out of, or in connection with, the use of this website. Please further review our Terms of Service.

