Macaulay Duration is a measure of the weighted average time before a bondholder receives the bond’s cash flows. It’s expressed in years and helps investors understand the sensitivity of a bond’s price to changes in interest rates. A higher Macaulay Duration indicates that the bond’s price is more sensitive to interest rate changes, implying a greater risk for longer-term investments. This Duration is particularly useful for bond portfolio managers and investors who need to manage the interest rate risk of their bond investments.
This page covers the following topics related to Macaulay Duration:
General Formula
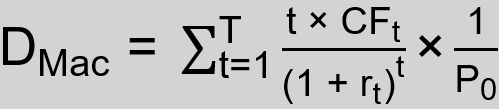
- Time in Years (t): Number of years until maturity T
- Cash Flow (CFt): Cash flow at year t
- Discount Rate (rt): Discount rate in year t
- Bond Price (P0): Price of the bond in year 0
The Macaulay Duration formula calculates the present value of each cash flow (interest and principal payments) multiplied by the time period in which it is received, then sums these values and divides by the present value of the bond. The time periods are weighted according to the proportion of the bond’s present value that each period’s cash flow represents.
Further, the Macaulay Duration is important for investors who want to match their investment horizons to their liabilities or those looking to manage the interest rate risk. A bond’s duration changes over time as it gets closer to maturity and as interest rates fluctuate. It’s more relevant for bonds with fixed interest payments than for those with variable rates.
Zero Bonds
DMac = T
A zero bond, also known as a zero-coupon bond, is a debt security that does not pay periodic interest. Instead, it is issued at a significant discount to its face value and pays its full face value at maturity. The Macaulay Duration of a zero bond is equal to its time to maturity (T), as it involves a single cash flow at maturity, simplifying the duration calculation to just the time remaining until the bond’s maturity date.
Application in Excel
To compute the Macaulay Duration using Excel, it is essential to first determine the bond’s yield to maturity by calculating its price. In the provided example, the bond price is ascertainable using the SUMPRODUCT(array1, [array2], [array3], …) function. This function should be used on the bond cash flows, which are located in cells B8:F8, and the discount factors, expressed as 1/(1+r)^t, found in cells B11:F11. The bond price is determined as follows:
=SUMPRODUCT(B8:F8,B11:F11)

The next step involves calculating the yield to maturity using Excel’s YIELD(settlement, maturity, rate, pr, redemption, frequency, [basis]) function. In cases where dates for ’settlement‘ or ‚maturity‘ are not available, the DATE(year, month, day) function can be utilized to establish a settlement date and a maturity date, ensuring they are spaced five years apart. The ‚rate‘ in this context is the coupon value located in cell B3, while ‚pr‘ refers to the bond price previously calculated in cell B15. ‚Redemption‘ is represented by the face value in cell B1, and ‚frequency‘ indicates the annual number of coupon payments, set at 1 in this instance. The formula for our example is as follows:
=YIELD(DATE(0,1,1),DATE(B2,1,1),B3,B15,B1,1)

The Macaulay Duration is determined using Excel’s DURATION(settlement, maturity, coupon, yld, frequency, [basis]) function. The formula for calculating the Macaulay Duration is structured similarly to the YIELD function. In this case, ‚yld‘ refers to the yield to maturity that was computed in the previous step and is available in cell B17.
=DURATION(DATE(0,1,1),DATE(B2,1,1),B2,B17,1)
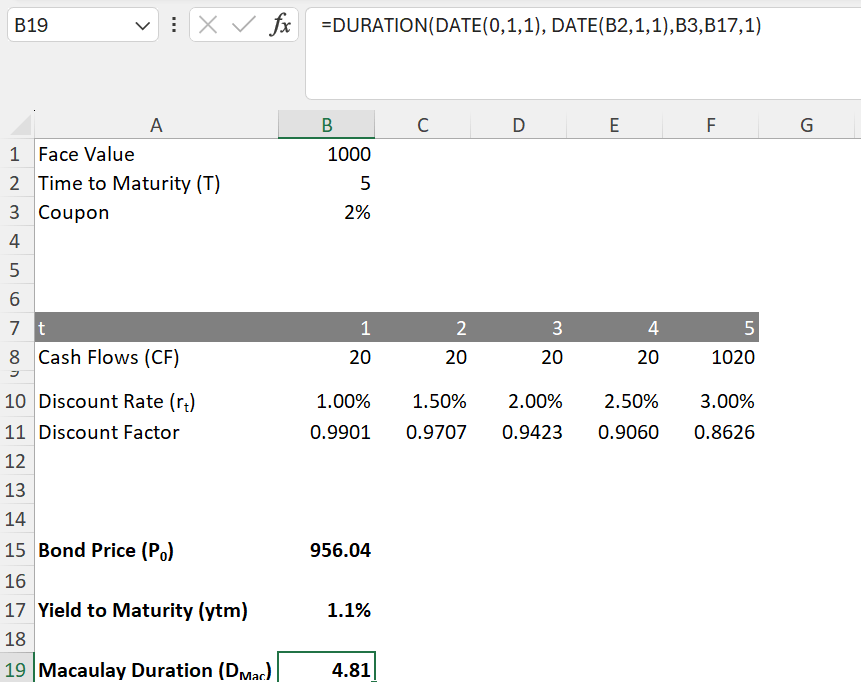
This will give you the Macaulay Duration of 4.81 in years. The Macaulay Duration is a fundamental concept in fixed-income investing and crucial for understanding the bond price’s sensitivity to interest rate changes.
Related Topics
Disclaimer: The information provided on this website is for educational purposes only and is not intended for use as legal, financial, or tax advice. While every effort is made to ensure the accuracy and reliability of the content, Maths for Finance makes no representations or warranties of any kind, express or implied, about the completeness, accuracy, reliability, suitability, or availability with respect to the website or the information, products, services, or related graphics contained on the website for any purpose. Any reliance you place on such information is therefore strictly at your own risk. In no event will Maths for Finance be liable for any loss or damage including without limitation, indirect or consequential loss or damage, or any loss or damage whatsoever arising from loss of data or profits arising out of, or in connection with, the use of this website. Please further review our Terms of Service.

