Modified Duration is a critical financial metric used to assess the sensitivity of a bond’s price to interest rate changes. It builds upon the concept of Macaulay Duration, adjusting it to directly relate to changes in yield to maturity. In essence, it measures how much the price of a bond is expected to change for a 1% change in interest rates. This metric is invaluable for portfolio managers and investors in gauging interest rate risk. Generally, a higher modified duration indicates greater sensitivity to interest rate changes, implying higher risk and potential return.
This page covers the following topics related to modified duration:
General Formula
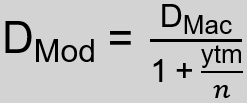
- Macaulay Duration (DMac): Weighted average time until a bond’s cash flows (i.e. interest and principal payments) are repaid
- Yield to Maturity (ytm): Return anticipated if bond is held until it matures
- Number of Coupon Periods per Year (n) number of coupon payments per year
The modified duration extends the concept of Macaulay Duration by accounting for yield to maturity, making it a more practical tool for measuring a bond’s interest rate risk. Whilst Macaulay Duration calculates the weighted average time until a bond’s cash flows are received, the Modified Duration adjusts Macaulay Duration to measure a bond’s price sensitivity to interest rate changes. It’s especially useful in a fluctuating interest rate environment, as it helps in predicting the potential impact of rate changes on a bond’s price.
Yield to Maturity
Yield to Maturity (ytm) is the internal rate of return of a bond, incorporating all coupon payments and the redemption at maturity. It usually cannot be numerically solved in a straightforward manner due to its definition as a solution to a polynomial equation in interest rates, necessitating iterative approximation methods for computation.

- Present Value (PV): Today’s value of the zero-coupon bond
- Face Value: Amount the bond will be worth at maturity (its par value)
- Yield to Maturity (ytm): Return anticipated if bond is held until it matures
- Total number of years (T): Number of years until the bond matures
- Coupon Payments (Ct): Payments paid to bondholder in each holding period t
Application in Excel
To calculate Modified Duration in Excel, one first needs to calculate the bond price to obtain the yield to maturity. In the example below, the bond price can be determined with the SUMPRODUCT(array1, [array2], [array3], …) function applied to the bond cash flows in cells B8:F8 and the discount factors (1/(1+r)^t) in cells B11:F11:
=SUMPRODUCT(B8:F8,B11:F11)

As a next step, the yield to maturity can be calculated with the YIELD(settlement, maturity, rate, pr, redemption, frequency, [basis]) function in Excel. If there is no date for ’settlement‘ or ‚maturity‘ available, one can use the DATE(year, month, day) function to define a settlement date and a maturity date, which are 5 years apart. Further, the ‚rate‘ refers to the coupon in cell B3 and the ‚pr‘ to the calculated bond price in cell B15. Moreover, ‚redemption‘ describes the face value in cell B1 and ‚frequency‘ the number of coupon payments per year of 1. In our example the formula is as follows:
=YIELD(DATE(0,1,1),DATE(B2,1,1),B3,B15,B1,1)

The modified duration can the be calculated by applying the MDURATION(settlement, maturity, coupon, yld, frequency, [basis]) function. The formula follows a similar logic compared to the YIELD function, whilst ‚yld‘ describes the calculated yield to maturity in the previous step in cell B17:
=MDURATION(DATE(0,1,1),DATE(B2,1,1),B3,B17,1)

This Excel function determines a modified duration of 4.76. The calculated modified duration can help investors understand how the bond’s price will move with interest rate changes.
Related Topics
Disclaimer: The information provided on this website is for educational purposes only and is not intended for use as legal, financial, or tax advice. While every effort is made to ensure the accuracy and reliability of the content, Maths for Finance makes no representations or warranties of any kind, express or implied, about the completeness, accuracy, reliability, suitability, or availability with respect to the website or the information, products, services, or related graphics contained on the website for any purpose. Any reliance you place on such information is therefore strictly at your own risk. In no event will Maths for Finance be liable for any loss or damage including without limitation, indirect or consequential loss or damage, or any loss or damage whatsoever arising from loss of data or profits arising out of, or in connection with, the use of this website. Please further review our Terms of Service.

